Clustering Algorithms Overview

Kōji offers two clustering algorithms, the fastest is a Rust translation of the FastCover-PP algorithm by ghoshanirban (opens in a new tab), the other is a Greedy algorithm that leverages the r-tree implentation from the rstar (opens in a new tab) crate. The latter algorithm offers different levels of complexity that vary in time, resource usage, and final performance.

Goal

The primary goal of Kōji's clustering algorithms is to cover the most number of data points with the fewest number of clusters of a given radius. However, many users of this app have slight variations of this goal in mind, which is why Kōji offers many different inputs to customize the final result.

Inputs

Data Points

The points to be clustered.

All algorithms accepts Vec<[f64;2]>
[Latitude, Longitude] pairs

Radius

The radius of each cluster to encase the data_points within, in meters.

Min Points

The minimum number of data_points that a cluster must contain to be considered valid

Max Clusters

The maximum number of clusters that should be generated

Unavailable when running the Fastest algorithm
Generally based on external factors for the user, such as the number of devices available to scan the route
Since the Greedy algorithm works down from the best clusters to the worst, when the desired max is hit, the algorithm will stop and return the best result possible for the set limit

Cluster Split Level

This input groups data_points based on their S2 cell level before clustering them. The groups are then run on separate threads in order to help with parallelizing workloads. e.g. if a user inputs a cluster_split_level of 10, then all of the data_points that are in unique level 10 S2 cells will be split up and clustered separately.

⚠️

This was more relevant with the legacy clustering algorithms that were single threaded but can still be useful in some cases

Metrics

To compare the performance of multiple algorithms the normalized mygod_score system is used, aptly named after a colleague who came up with it. This score is calculated by multiplying the number of clusters by the min_points input added to the difference of the total input_points and the number of data_points that were covered by the algorithm. This incentives the algorithms to cover the maximum number of data_points possible but only if the clusters cover a number of unique data_points that is greater than or equal to the set min_points. The lower the score, the better the result.

pub fn get_score(&self, min_points: usize) -> usize {
      self.total_clusters * min_points + (self.total_points - self.points_covered)
}

Runtime is not a factor in the mygod_score because it is not the primary goal of Kōji's userbase. Though it does make development time less painful and is a small factor for some external integrations that can't be waiting around for more than several minutes for a result. In the future, if the algorithm ever gets to a point where it's final results are near perfect, then time may be added to the mygod_score calculation for further refinement.

Algorithm Details

Unit Disc Cover (UDC)

Source (opens in a new tab)

The UDC algorithm is mostly a classic implementation of the UDC problem and is not particularly written for Kōji. While it is much faster, it does not produce an optimal result. It often leads to a lot of overlap between clusters and does not take into account the density of data_points in a given area. This algorithm is best used when the user is looking for a quick result and does not care about the quality of the result. Since it is less specialized for the task at hand, the inputs are mostly taken into account during pre and post processing functions. On its own, this algorithm does not take into account the spherical nature of the Earth, so as part of the pre-process function, the input data_points must be projected onto a flat plane that takes the input radius into account. The post-process function then takes the projected data_points and converts them back to their original spherical coordinates. You can read more about UDC here (opens in a new tab).

Greedy

Source (opens in a new tab)

The Greedy algorithm on the other hand is much more specialized for the task at hand. Compared to its predecessors, it leverages an r-tree algorithm that allows it to run faster than the O(n^2) time complexity that the legacy algorithms could not achieve. This algorithm has three different levels of complexity that user's can select from. Fast, Balanced, and Better. The only difference between these options is the number of potential clusters that are generated based on the input data_points.

Step 1 - Generate Potential Clusters

Source (opens in a new tab)

Here is where the algorithm complexity input is utilized.

let potential_clusters: Vec<Cluster> = match cluster_mode {
      ClusterMode::Better | ClusterMode::Best => get_s2_clusters(points),
      ClusterMode::Fast => gen_estimated_clusters(&point_tree),
      _ => {
            let neighbor_tree: RTree<Point> = rtree::spawn(radius * 2., points);
            gen_estimated_clusters(&neighbor_tree)
      }
}

Fast: Generates possible clusters at the provided data_points and at 8 equal segments between a given point and its neighbors that are within the given radius.
Balanced: Similar logic to Fast but generates the same 8 equal segments between the given point and its neighbors that are within the radius * 2. Additionally, it adds some "wiggle" data_points at each of the segments.
Better: This option leverages the Rust S2 library (opens in a new tab) and generates a potential cluster at every level 22 S2 cell that is within the BBOX of the input data_points. This is the most resource intensive option but produces the best result. This process has been optimized by starting at level 16 and continueing to split cells down to level 22 in parallel using Rayon (opens in a new tab).

Step 2 - Associate Potential Clusters

Source (opens in a new tab)

Now that the potential clusters have been generated, they need to be associated with the input data_points. This is where the primary use of the r-tree is implemented and has saved us the most time compared to the legacy algorithms. Even though this step utilizes Rayon to parallelize the workload, it is still the most expensive part of the algorithm and has the most room for improvement. The r-tree is used to find all data_points that are within the radius of a given potential cluster. This is done in parallel for all potential clusters. It also has to check to see if the cluster exists in the r-tree, in the case that the best cluster is indeed a point itself. If the cluster has less data_points than the given min_points input, the cluster is removed from the list of potential clusters, allowing us to release as much memory as possible and save some time in the clustering step.

let clusters_with_data: Vec<Cluster> = potential_clusters
      .into_par_iter()
      .filter_map(|cluster| {
            // Get the associated points
            let mut points: Vec<&Point> = point_tree
                  .locate_all_at_point(&cluster.center)
                  .collect::<Vec<&Point>>();
            // Check if the cluster is a point
            if let Some(point) = point_tree.locate_at_point(&cluster.center) {
                  points.push(point);
            }
            if points.len() < min_points {
                  // Skip it if we're never going to be interested in it anyway
                  None
            } else {
                  Some(Cluster::new(cluster, points, vec![]))
            }
      })
      .collect();

Step 3 - Cluster the Clusters

Source (opens in a new tab)

In this step the clusters are being grouped by the number of data_points that they cover. This helps us save some time during the clustering step.

// Finds the max number of points that a cluster covers
let max = clusters_with_data
      .par_iter()
      .map(|cluster| cluster.all.len())
      .max()
      // For the users of Kōji there will likely never be anything higher than 100 points in a cluster
      .unwrap_or(100);
 
// Creates a new Vec, filled with Vecs with the size set to the max number of points that a cluster covers
// plus one, because we want to skip the 0 index for convenience
let mut clustered_clusters = vec![vec![]; max + 1];
for cluster in clusters_with_data.into_iter() {
      clustered_clusters[cluster.all.len()].push(cluster);
}

Step 4 - Clustering

Source (opens in a new tab)

This section is broken down into sub steps and will only contain summarized code snippets to avoid copying and pasting the entire function, each section will have links to the original source code.

Step 4a - Setup

Source (opens in a new tab)

Start by setting up the mutable variables that help us keep track of where things are during the while loop runs.

new_clusters: A HashSet that will hold the picked clusters. The Cluster struct implement the Hash trait and are hashed based on the S2 Cell ID of the center point. Despite the Cluster struct being a complex type, it was unnecessary to use a HashMap because it's not necessary to access the data by key, only making sure that duplicates are not inserted.
blocked_points: an additional HashSet that is keeping track of data_points that have already been clustered, to ensure that the algorithm is not double counting data_points that are covered by multiple clusters.
current: a var that starts at the max number of data_points that a cluster covers and is decremented until it reaches the min_points input.
The rest of the variables are for tracking how much time is spent on each step and for estimating the % complete in the logs.

The rest of the steps occur in the while loop.

Step 4b - Get Interested Clusters

Source (opens in a new tab)

This step is where clusters that have the number of data_points that the current iteration is interested in are filtered. Since this algorithm is greedy, it starts at the highest and works its way down to the min_points input. This is why the algorithm grouped its potential clusters in step 3. This is a very simple loop that checks whether the index of each item is greater than or equal to the current var. If it is, it's added to the clusters_of_interest Vec. The reason to go with greater than or equal to is because the algorithm will continue to filter the clusters later on. Just because a cluster didn't end up being viable when current is equal to 42, is still may be the best when current is equal to 30.

for (index, clusters) in clusters_with_data.iter().enumerate() {
      if index < current {
            continue;
      }
      clusters_of_interest.extend(clusters);
}

Step 4c - Filtering Clusters

Source (opens in a new tab)

The algorithm will now filter out clusters that are not viable. Iterating through clusters_of_interest in parallel, it checks how many data_points for each one have already been clustered, if the total is less than current, it is discarded. During this step it is ensuring two important Vecs for each cluster, all of the data_points that it covers and the unique number of points that it could potentially be responsible for.

If the determined local_clusters is empty, it subtracts one from current and start the next iteration. If not, it then sorts the clusters in parallel by the number of data_points that they cover. If the total data_points between any two given clusters is equal, then it compares the unique number of data_points that they cover. This is important for the next step because it will be iterating through the clusters in serial and it's important to get the best cluster before it starts discarding.

Step 4d - Looping and Pushing to the `new_clusters` HashSet

Source (opens in a new tab)

Iterate through local_clusters in serial and push the best cluster to the new_clusters HashSet.

At the start of the loop, it checks to see if the number of clusters it has already saved is greater than or equal to the max_clusters input and immediately break the entire while loop if so.
Next it checks every unique point that the cluster is responsible for to see if it has already been clustered, if so, skips it. This is why sorting them before this step is important.
If the cluster passes, then it inserts all of the unique data_points into the blocked_points HashSet and the cluster into the new_clusters HashSet.

if cluster.points.len() >= current {
      for point in cluster.points.iter() {
            if blocked_points.contains(point) {
                  continue 'cluster;
            }
      }
      for point in cluster.points.iter() {
            blocked_points.insert(point);
      }
      new_clusters.insert(cluster);
}

Step 4e - Decrement `current` and Repeat

Lastly it subtracts 1 from the current var and continue to run the next iteration of loop while current is greater than or equal to the min_points input and the length of new_clusters is less than the max_clusters input.

Step 5 - Unique Point Coverage Check

Source (opens in a new tab)

Now that the algorithm has gathered the full list of preliminary clusters, it needs to make sure that each cluster is responsible for a unique number of points that is greater than or equal to the min_points input.

Create a new r-tree with the potential clusters
Iterate through the mutable clusters in parallel
Via the update_unique trait, it then iterate through all of the data_points that the cluster covers and determine if a point is unique to that cluster by how many clusters are found at the point's location in the r-tree. If the number of clusters is equal to one, it knows that the point is unique to that cluster.
Filter out the clusters that do not have a unique number of data_points that is greater than or equal to the min_points input.

pub fn update_unique(&mut self, tree: &RTree<Point>) {
      let mut points: Vec<_> = self
            .all
            .par_iter()
            .filter_map(|p| {
                  if tree.locate_all_at_point(&p.center).count() == 1 {
                        Some(*p)
                  } else {
                        None
                  }
            })
            .collect();
      points.sort_dedupe();
      self.points = points;
}

Step 6 - Check for Missing

Source (opens in a new tab)

If the min_points input is equal to one, it wants to make absolutely sure that no point has been missed as this is most often used in requests that require 100% accuracy. This step is often unnecessary, and is currently considered a bandaid that fixes a possible issue with the earlier clustering process.

First it reduces all data_points covered by the clusters into a single HashSet
Next if the length of the HashSet does not equal the length of the input data_points, it knows that at least one point has been missed.
Then iterate through the input data_points, checking to see which ones exist in the HashSet, saving the ones that do not.
Finally, extend the current clusters with the missing ones.

Balanced (Legacy)

⚠️

The code has now been removed from the codebase as it does not provide any benefit but the source is still viewable (opens in a new tab).

This algorithm was not the first one written for Kōji but it was the first that was committed to the codebase. It operated in at least O(n^2) time, was single threaded, and was total spaghetti. The core of it is based on what Kōji calls "Bootstrapping", which generates circles of a given radius inside of a given Polygon or MultiPolygon to cover the entire area, allowing for routes that pick up all Spawnpoints and Forts.

Concept wise, it was very similar to how Greedy operates now and it ran decently well for creating Fort routes but did not have the logic required to work well with Spawnpoints. It attempted to take what was learned from translating the UDC algorithm and apply it to this algorithm, particularly when it came to combining clusters, since a honeycomb base allowed me to predict which neighboring clusters existed, similar to UDC. However, merging clusters tends to be very tedious work and was prone to errors.

Brute Force (Legacy)

⚠️

The code has now been removed from the codebase as it does not provide any benefit but the source is still viewable (opens in a new tab).

Shortly before starting work on this algorithm, I had completed the integration with OR-Tools, which utilizes a distance matrix in the C++ wrapper. I attempted to apply that same logic here as a sort of lookup table for checking which data_points are within the given radius of neighboring data_points, and since the values weren't reliant on each other, this calculation could be parallelized with Rayon. The core clustering algorithm is very recognizable as it was the base of the Greedy algorithm. However, it was still slower than what I had hoped for and my attempt to write another merge function wasn't very successful.

Result Comparisons

Distance stats have been excluded from each result as the data_points were unsorted and it is not relevant for directly comparing the clustering algorithms.
All algorithms were run on a MacBook Pro M1 with 16GB of RAM and 8 cores.
The following inputs were used:
- min_points: 3
- radius: 70
- cluster_split_level: 1

Small Fence

Info

Data Points: 11,064
Area: 84,432 km²

Results

# Fastest
[STATS] =================================================================
|| [POINTS] Total: 11064 | Covered: 10861                              ||
|| [CLUSTERS] Total: 1361 | Avg Points: 7                              ||
|| [BEST_CLUSTER] Amount: 1 | Point Count: 35                          ||
|| [TIMES] Clustering: 0.02s | Routing: 0.00s | Stats: 0.07s           ||
|| [MYGOD_SCORE] 4286                                                  ||
=========================================================================

# Balanced (Legacy)
[STATS] =================================================================
|| [POINTS] Total: 11064 | Covered: 10995                              ||
|| [CLUSTERS] Total: 1196 | Avg Points: 9                              ||
|| [BEST_CLUSTER] Amount: 1 | Point Count: 32                          ||
|| [TIMES] Clustering: 4.11s | Routing: 0.00s | Stats: 0.06s           ||
|| [MYGOD_SCORE] 3657                                                  ||
=========================================================================

# Brute Force (Legacy)
[STATS] =================================================================
|| [POINTS] Total: 11064 | Covered: 10442                              ||
|| [CLUSTERS] Total: 931 | Avg Points: 11                              ||
|| [BEST_CLUSTER] Amount: 1 | Point Count: 43                          ||
|| [TIMES] Clustering: 8.23s | Routing: 0.00s | Stats: 0.06s           ||
|| [MYGOD_SCORE] 3415                                                  ||
=========================================================================

# Fast
[STATS] =================================================================
|| [POINTS] Total: 11064 | Covered: 10629                              ||
|| [CLUSTERS] Total: 856 | Avg Points: 12                              ||
|| [BEST_CLUSTER] Amount: 1 | Point Count: 45                          ||
|| [TIMES] Clustering: 0.41s | Routing: 0.00s | Stats: 0.04s           ||
|| [MYGOD_SCORE] 3003                                                  ||
=========================================================================

# Balanced
[STATS] =================================================================
|| [POINTS] Total: 11064 | Covered: 10712                              ||
|| [CLUSTERS] Total: 854 | Avg Points: 12                              ||
|| [BEST_CLUSTER] Amount: 1 | Point Count: 44                          ||
|| [TIMES] Clustering: 1.13s | Routing: 0.00s | Stats: 0.05s           ||
|| [MYGOD_SCORE] 2914                                                  ||
=========================================================================

# Better
[STATS] =================================================================
|| [POINTS] Total: 11064 | Covered: 10715                              ||
|| [CLUSTERS] Total: 828 | Avg Points: 12                              ||
|| [BEST_CLUSTER] Amount: 1 | Point Count: 45                          ||
|| [TIMES] Clustering: 8.18s | Routing: 0.00s | Stats: 0.05s           ||
|| [MYGOD_SCORE] 2833                                                  ||
=========================================================================

Medium Fence

Info

Data Points: 76,692
Area: 276,255 km²

Results

# Fastest
[STATS] =================================================================
|| [POINTS] Total: 76692 | Covered: 76189                              ||
|| [CLUSTERS] Total: 9540 | Avg Points: 7                              ||
|| [BEST_CLUSTER] Amount: 1 | Point Count: 42                          ||
|| [TIMES] Clustering: 0.10s | Routing: 0.00s | Stats: 0.40s           ||
|| [MYGOD_SCORE] 29123                                                 ||
=========================================================================

# Balanced (Legacy)
[STATS] =================================================================
|| [POINTS] Total: 76692 | Covered: 76576                              ||
|| [CLUSTERS] Total: 8314 | Avg Points: 9                              ||
|| [BEST_CLUSTER] Amount: 2 | Point Count: 39                          ||
|| [DISTANCE] Total: 1731728m | Longest: 17861m | Avg: 208m            ||
|| [TIMES] Clustering: 206.22s | Routing: 0.00s | Stats: 0.50s         ||
|| [MYGOD_SCORE] 25058                                                 ||
=========================================================================

# Brute Force (Legacy)
[STATS] =================================================================
|| [POINTS] Total: 76692 | Covered: 72854                              ||
|| [CLUSTERS] Total: 6563 | Avg Points: 11                             ||
|| [BEST_CLUSTER] Amount: 1 | Point Count: 52                          ||
|| [TIMES] Clustering: 489.92s | Routing: 0.00s | Stats: 0.49s         ||
|| [MYGOD_SCORE] 23527                                                 ||
=========================================================================

# Fast
[STATS] =================================================================
|| [POINTS] Total: 76692 | Covered: 73880                              ||
|| [CLUSTERS] Total: 5836 | Avg Points: 12                             ||
|| [BEST_CLUSTER] Amount: 1 | Point Count: 53                          ||
|| [TIMES] Clustering: 2.42s | Routing: 0.00s | Stats: 0.40s           ||
|| [MYGOD_SCORE] 20320                                                 ||
=========================================================================

# Balanced
[STATS] =================================================================
|| [POINTS] Total: 76692 | Covered: 74551                              ||
|| [CLUSTERS] Total: 5821 | Avg Points: 12                             ||
|| [BEST_CLUSTER] Amount: 1 | Point Count: 53                          ||
|| [TIMES] Clustering: 8.20s | Routing: 0.00s | Stats: 0.40s           ||
|| [MYGOD_SCORE] 19604                                                 ||
=========================================================================

# Better
[STATS] =================================================================
|| [POINTS] Total: 76692 | Covered: 74641                              ||
|| [CLUSTERS] Total: 5690 | Avg Points: 13                             ||
|| [BEST_CLUSTER] Amount: 1 | Point Count: 54                          ||
|| [TIMES] Clustering: 41.46s | Routing: 0.00s | Stats: 0.40s          ||
|| [MYGOD_SCORE] 19121                                                 ||
=========================================================================

Large Fence

Info

Points: 169,038
Area: 754,594 km²
Both of the legacy algorithms have been excluded from this example due to the amount of time it would take to run them.

Results

# Fastest
[STATS] =================================================================
|| [POINTS] Total: 169038 | Covered: 167788                            ||
|| [CLUSTERS] Total: 21931 | Avg Points: 7                             ||
|| [BEST_CLUSTER] Amount: 3 | Point Count: 39                          ||
|| [TIMES] Clustering: 0.20s | Routing: 0.00s | Stats: 0.95s           ||
|| [MYGOD_SCORE] 67043                                                 ||
=========================================================================

# Fast
[STATS] =================================================================
|| [POINTS] Total: 169038 | Covered: 162747                            ||
|| [CLUSTERS] Total: 13554 | Avg Points: 12                            ||
|| [BEST_CLUSTER] Amount: 1 | Point Count: 48                          ||
|| [TIMES] Clustering: 6.48s | Routing: 0.00s | Stats: 0.92s           ||
|| [MYGOD_SCORE] 46953                                                 ||
=========================================================================

# Balanced
[STATS] =================================================================
|| [POINTS] Total: 169038 | Covered: 164028                            ||
|| [CLUSTERS] Total: 13358 | Avg Points: 12                            ||
|| [BEST_CLUSTER] Amount: 1 | Point Count: 47                          ||
|| [TIMES] Clustering: 21.16s | Routing: 0.00s | Stats: 0.94s          ||
|| [MYGOD_SCORE] 45084                                                 ||
=========================================================================

# Better
[STATS] =================================================================
|| [POINTS] Total: 169038 | Covered: 164297                            ||
|| [CLUSTERS] Total: 13048 | Avg Points: 12                            ||
|| [BEST_CLUSTER] Amount: 1 | Point Count: 49                          ||
|| [TIMES] Clustering: 125.90s | Routing: 0.00s | Stats: 0.94s         ||
|| [MYGOD_SCORE] 43885                                                 ||
=========================================================================

Conclusion

Fence	Algorithm	Time (s)	Score
Small	Fastest	0.02	4,286
Small	Balanced (L)	4.11	3,657
Small	Brute Force (L)	8.23	3,415
Small	Fast	0.41	3,003
Small	Balanced	1.13	2,914
Small	Better	8.18	2,833
Medium	Fastest	0.10	29,123
Medium	Balanced (L)	206.22	25,058
Medium	Brute Force (L)	489.92	23,527
Medium	Fast	2.42	20,320
Medium	Balanced	8.20	19,604
Medium	Better	41.46	19,121
Large	Fastest	0.20	67,043
Large	Fast	6.48	46,953
Large	Balanced	21.16	45,084
Large	Better	125.90	43,885

While the different variations of the Greedy algorithm don't scale as well as the UDC algorithm, the results are definitely worth it, especially compared to both of the legacy algorithms, which start to become unweildly on anything but smaller sizes fences.

The legacy Balanced algorithm showing off its honeycomb approach and inefficiencies.

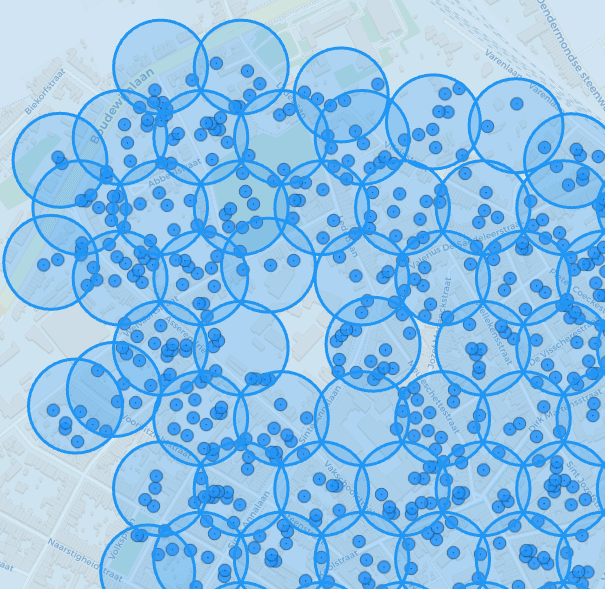
The legacy BruteForce algorithm, take note of the blue circle that was added to demonstrate that it missed a valid cluster.

The Fastest algorithm is great for quick and dirty calculations that want to cover everything and you need the results immediately.

The Fast algorithm is if you want to take advantage of the Greedy algorithm but still need the results very quickly and can't wait for Balanced or Better.

The Balanced algorithm is a great balance of speed and result quality. It is the default algorithm that Kōji uses and is recommended for most users.

The Better algorithm is for when you want the best result possible and are willing to wait for it. It is the most resource intensive and can take a long time to run on larger fences. Not recommend for systems that do not have much free memory.

Future work

The two biggest improvements that can be made to the Greedy algorithm are:

Optimize Potential Cluster Generating

Currently this process takes up the bulk of the algorithm time. It also is a huge resource hog that actually makes it impossible to run Better on areas that are too big if the machine can't handle it.

Additional Post processing

Implementing a Genetic Algorithm (opens in a new tab) approach that further optimizes the intial solution.

This could be accomplished by first associating clusters with each other by utilizing the r-tree nearest neighbor methods and all of their respective data_points.
Once the subgroups have been created, try different combination of clusters and see if the mygod_score can be improved at all by trying different combinations of clusters.

Example

If you had a group of 14 data_points with a min_points of 3, but you have one cluster covering the middle 10, then 2 on either side of that cluster. In this situation, replacing the single centric cluster with two clusters to cover all 14 data_points would result in an improved mygod_score.

Scripts Integrations

Clustering Algorithms Overview

Goal

Inputs

Data Points

Radius

Min Points

Max Clusters

Cluster Split Level

Metrics

Algorithm Details

Unit Disc Cover (UDC)

Greedy

Step 1 - Generate Potential Clusters

Step 2 - Associate Potential Clusters

Step 3 - Cluster the Clusters

Step 4 - Clustering

Step 4a - Setup

Step 4b - Get Interested Clusters

Step 4c - Filtering Clusters

Step 4d - Looping and Pushing to the new_clusters HashSet

Step 4e - Decrement current and Repeat

Step 5 - Unique Point Coverage Check

Step 6 - Check for Missing

Balanced (Legacy)

Brute Force (Legacy)

Result Comparisons

Small Fence

Info

Results

Medium Fence

Info

Results

Large Fence

Info

Results

Conclusion

Future work

Optimize Potential Cluster Generating

Additional Post processing

Example

Step 4d - Looping and Pushing to the `new_clusters` HashSet

Step 4e - Decrement `current` and Repeat